[Retranscription de la litographie d'une des premières leçons d'économie pure tenues par Vilfredo Pareto à l'Université de Lausanne, probablement celle du 22 mai 1893]

Publié in: History of Economics Ideas, vol. 5, no. 3, 1997

Transformation des biens économiques

Les biens économiques peuvent le plus souvent se transformer, pour un homme, les uns dans les autres.
Les moyens par lesquels s'exécutent ordinairement ces transformations sont : L'échange, et la production. Quand il s'agit du phénomène de l'échange, on ne saurait évidemment considérer un homme seul. Les échangeurs réagissent les uns sur les autres. Mais rien n'empêche que, comme simple procédé de raisonnement, on considère d'abord un des échangeurs, et puis l'autre. C'est un procédé analytique en usage dans toutes les sciences. M. Walras le suit en supposant qu'on crie au hasard des prix sur le marché, et en observant ce qui arrive alors de chaque échangeur. Il est parvenu de la sorte à porter une grande rigueur et une grande clarté dans une matière assez difficile.
Il y a deux problèmes à résoudre :
1) Les proportions dans lesquelles un individu peut transformer un bien économique dans un autre ayant été criées au hasard, ou fixées de quelque autre manière, que nous ne précisons pas, quelles transformations seront accomplies par cet individu?
2) Comment s'établiront ces proportions, quand elles résulteront de l'échange libre de deux, ou de plusieurs individus?
Nous traiterons d'abord le premier problème, qui appartient à l'économie individuelle. Le second problème est celui de l'échange de plusieurs marchandises.
Parmi les biens économiques il en est un : Le travail, qui est le plus généralement transformé en d'autres biens. C'est peut-être pour cela que plusieurs économistes ont cru voir dans le travail la source de ce qu'ils appelaient la valeur. Nous reviendrons sur ce sujet. Ici, il nous suffit de noter que le travail est un bien économique parce qu'il est rare, et que quand on obtient des utilités au moyen du travail on ne fait que transformer des utilités les unes dans les autres.

Loi de la variété des besoins humains

Les besoins des hommes sont variés, et illimités. On peut donc avoir trop d'un certain bien économique, et l'on peut désirer le transformer en d'autres, mais l'on ne saurait avoir trop de tous les biens économiques.
Quand nos besoins les plus urgents sont satisfaits nous pensons à satisfaire les moins urgents, et quand ceux-ci sont à leur tour éteints, il en naît d'autres, et d'autres encore, à l'infini.
Un ouvrier qui ne trouve pas d'ouvrage est un homme qui a en excès un bien économique (le travail) et qui ne trouve pas moyen de le transformer en d'autres biens économiques dont il manque.
Un cultivateur qui a beaucoup de bétail et peu de foin a encore un excès d'un bien économique par rapport à un autre.
Ce n'est jamais l'excès des biens économiques qui peut produire la souffrance de la personne qui les possède. C'est seulement la difficulté qu'elle éprouve, par des causes naturelles ou artificielles, à transformer ses biens économiques, qui peut nuire à cette personne.

Théorème et formule de M. Walras

Le théorème de M. Walras est fondamental. Toute l'économie politique pure n'en est qu'un développement. Commençons par un problème très simple.
Un individu a du vin et n'a pas de vinaigre. On connaît la quantité de vin que cet individu possède, ainsi que les courbes d'utilité, ou de besoin, pour lui, du vin et du vinaigre. L'on demande quelle quantité de vin cet individu transformera en vinaigre. On admet : 1) qu'une unité de vin se transforme dans une unité de vinaigre. 2) que l'on peut négliger la peine qu'il faut prendre pour transformer le vin en vinaigre, et la perte de temps. Les quantités de vin et de vinaigre considérées peuvent être des quantités journalières, mensuelles, etc ... .
Observons d'abord que si la rareté du vin est plus grande que la rareté du vinaigre, aucune transformation n'aura lieu.

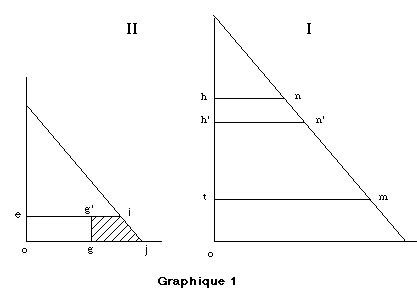
I est la courbe d'utilité du vin. II est la courbe d'utilité du vinaigre. Si la quantité de vin possédée est ot la rareté sera tm. La rareté du vinaigre, quand l'individu n'en a pas du tout, est oj , et si tm est plus grand que oj , il n'y a pas de transformation de vin en vinaigre.
Supposons que la quantité de vin possédée soit oh, et que la rareté correspondante hn soit plus petite que oj . Alors la transformation aura lieu.
Si l'individu transforme une très petite quantité de vin, par exemple un centilitre, en vinaigre, il renoncera au plaisir mesuré par la surface hnn'h'. La longueur hh' représentant un centilitre. Mais l'individu gagne, en échange, le plaisir représenté par la surface ojie , c'est à dire le plaisir de consommer un centilitre de vinaigre; oe étant égal à un centilitre, comme hh'. L'individu considéré bénéficie de la différence entre le plaisir qu'il gagne et celui qu'il perd. Cette différence est représentée par la surface geig' . La longueur og étant égale à hn.
La transformation continuera évidemment jusqu'à ce que le plaisir que gagne l'individu par la consommation du vinaigre ne soit égal au plaisir auquel il renonce en diminuant encore sa consommation de vin. C'est à dire : la transformation s'arrêtera quand la rareté du vin sera égale à celle du vinaigre. C'est l'expression du théorème de M. Walras, dans ce cas particulier, extrêmement simple.

Si l'on porte la figure II sur la figure I, de manière que oj se trouve sur hn, le point M, où se rencontrent les courbes, est le point où les raretés deviennent égales toutes deux à MP. La quantité de vin transformée en vinaigre est représentée par hP; et notre problème est résolu.
Nous observons encore: 1) que, grâce à la transformation des biens économiques, l'individu s'est procuré un accroissement de plaisir, ou d'utilité, mesuré par la surface Mnj. 2) qu'en arrêtant la transformation précisément au point M, l'individu se procure le plus grand plaisir, ou la plus grande utilité, qu'elle soit susceptible de donner. Pour cette raison le théorème que nous venons d'exposer porte aussi le nom de théorème de la satisfaction maxima. D'autres auteurs ont fait connaître ce théorème en même temps que M. Walras. Mais ce qui appartient à M. Walras c'est d'avoir donné à ce théorème toute sa généralité, et d'en avoir fait connaître la merveilleuse fécondité.

Compliquons un peu plus notre problème en supposant que l'individu possède non seulement une certaine quantité de vin oh, mais encore une certaine quantité de vinaigre ok, et qu'il soit également possible de transformer le vin en vinaigre, et le vinaigre en vin.
Si hn est plus petit que kL (Fig.1) c'est la première transformation qui aura encore lieu. Au contraire si kL est plus petit que hn (Fig.2), c'est le vinaigre qui sera transformé en vin.
Dans les deux cas la transformation s'arrêtera au point M, quand la rareté du vin sera égale à la rareté du vinaigre.
Pour obtenir ce point M on portera kL sur hn, en renversant la courbe II (la quantité de vin décroît quand celle de vinaigre croît, et vice versa). Le point M d'intersection des deux courbes est le point où s'arrêtera la transformation. MP est la valeur commune de la rareté pour le vin et pour le vinaigre. La surface MnL représente le gain d'utilité que fait l'individu grâce à la transformation des biens économiques. Ph est la quantité de vin qui est transformée en vinaigre (Fig.1), ou bien de vinaigre qui est transformée en vin (Fig.2). Introduisons une nouvelle complication dans le problème. Supposons que l'unité de vin se transforme seulement en 1/2 unité de vinaigre. Il convient de donner un nom à cette proportion entre les quantités transformées. La quantité de vin qui se transforme dans l'unité de vinaigre sera dite le prix du vinaigre en vin. Si au lieu de vin nous considérions la monnaie, ce serait le prix ordinaire. Dans l'exemple que nous avons choisi ce prix est de 2. En général appelons-le p. Nous dirons alors que 1 de vin se transforme en 1/p de vinaigre, ou bien qu'il faut p de vin pour obtenir 1 de vinaigre.
Reprenons le raisonnement précédent. Nous supposerons, pour fixer les idées, que ce soit le vin qui se transforme en vinaigre. Une très petit quantité de vin, un centilitre par exemple, se réduira à moitié (à un demi centilitre), en se transformant en vinaigre. On continuera la transformation tant que le plaisir qu'on perd en renonçant à la consommation d'un centilitre de vin est plus petit que le plaisir que l'on gagne en augmentant sa consommation d'un demi centilitre de vinaigre; on s'arrêtera quand ces deux plaisirs seront égaux. Mais le premier est représenté par la rareté du vin multipliée par un centilitre, le second par la rareté du vinaigre multipliée par 1/2 centilitre. Donc on s'arrêtera quand la rareté du vin sera égale à la moitié de celle du vinaigre, en général à 1/p de celle du vinaigre, si le prix est p.

Voici comment on détermine les quantités transformées. Soit toujours II la courbe d'utilité du vinaigre, I celle du vin. Si l'individu transforme une petite quantité hh' de vin en vinaigre, il perd encore l'utilité hh'n'n, mais il ne gagne plus, comme précédemment l'utilité aa'b'b (aa' étant égal à hh'), mais seulement la moitié, puisque 1 centilitre de vin donne seulement un demi centilitre de vinaigre. Pour lever cette difficulté transformons la courbe II de la manière suivante.
La courbe II peut être considérée comme résultant d'une suite de petits rectangles. Doublons la hauteur de ces rectangles, et pour que la surface demeure la même, réduisons à moitié la largeur; nous aurons ainsi la courbe III. Celle-ci nous représente non plus l'utilité directe du vinaigre, mais bien l'utilité du vin transformé en vinaigre. Maintenant nous n'avons plus qu'a reprendre mot à mot le raisonnement du cas précédent, en employant la courbe III au lieu de la courbe II. Soit oa la quantité de vinaigre possédée par l'individu. On prendra ok double de oa; on portera kL sur hn, le point M d'intersection de la courbe I, et de la courbe III renversée, sera le point où s'arrêtera la transformation. MP sera alors la rareté du vin, et la moitié de la rareté du vinaigre. hP sera la quantité de vin transformée en vinaigre. nML représentera le gain d'utilité que fait l'individu grâce à la transformation. Si le prix est p, la courbe II se transforme en multipliant par p les hauteurs, et en divisant par p les largeurs des rectangles ou, ce qui revient au même en multipliant par p les ordonnées et en divisant par p les abscisses. Le reste du raisonnement ne change pas.
On peut d'ailleurs supposer qu'au lieu de la courbe II on donne de suite la courbe III des utilités du vin transformé en vinaigre. Supposons que je note le plaisir que me procure un premier franc dépensé en tabac, puis un second franc, un troisième, etc.; j'aurai une courbe, analogue à III, qui m'indiquera l'utilité des francs transformés en tabac.
Laissons maintenant de côté le cas particulier du vin et du vinaigre, et raisonnons en général. Nommons (A), (B), (C), (D), ... des biens économiques en nombre quelconque. Le premier servira de numéraire. Les prix des autres seront donc exprimés en ce premier bien (A). Admettons qu'on puisse à volonté transformer (A) en (B), (C), (D) etc ... , ou bien (B), (C), (D) ... en (A). Soient : pb le prix de (B) en (A), pc le prix de (C) en (A) etc. Dans ce qui précède (A) était le vin, le vinaigre était (B), ou bien (C), ou bien (D) etc ... . Or nous avons vu que la transformation de (A) en (B), ou vice versa ne s'arrêtera que quand la rareté de (A) sera égale à la rareté de (B) divisée par le prix de (B) en (A). On peut dire exactement la même chose de la transformation de (A) en (C), (ou vice versa); et ainsi de suite pour tous les biens économiques comparés à (A). La rareté de chacun de ces biens divisée par le prix doit donner pour quotient la rareté de (A). En d'autres termes : Les transformations s'arrêteront quand les raretés seront proportionnelles aux prix. C'est le théorème de M. Walras dans toute sa généralité. Il faut faire attention : 1) Qu'il s'agit de prix criés au hasard, ou fixés arbitrairement, et non pas de prix courants. La détermination des prix courants est l'objet du second problème dont nous avons parlé. 2) que tous les biens économiques, sans exception, possédés par l'individu entrent dans cette formule.
On peut écrire cette formule de la manière suivante : Rareté de (A) égale rareté de (B) divisée par le prix de (B), égale rareté de (C) divisée par le prix de (C), égale etc.
Ou bien avec les symboles algébriques, qui veulent dire précisément la même chose

Si les biens économiques sont au nombre de m, les équations que nous venons d'écrire sont au nombre de m-1. Il faut en ajouter une autre :

qui indique que les biens économiques se sont simplement transformés les uns dans les autres, sans gain ni déchet sur les quantités. On a ainsi m équations, qui suffisent pour déterminer les m inconnues 

Supposons le prix exprimé en francs (seulement pour fixer les idées). La rareté divisée par le prix indique alors la quantité de rareté que l'on achète avec un franc. En vertu du théorème de M. Walras toutes les quantités de raretés qu'on achète avec un franc, quand cesse la transformation des biens économiques, doivent être égales. En d'autres termes : Les derniers besoins satisfaits au moyen de l'unité de monnaie doivent être égaux pour tous les biens économiques. Et c'est ainsi que l'individu se procure le maximum de bien être.
M. Walras a donné une démonstration géométrique très élégante de son théorème, dans le cas de plusieurs marchandises. C'est à cette démonstration que nous avons emprunté la transformation de la courbe d'utilité du vinaigre, quand le prix du vinaigre était 2.
Wicksteed exprime le théorème de M. Walras en disant : "Le père de famille, ou la bonne ménagère, cherchent à faire en sorte que le dernier sou (shilling, livre sterling, ou dans chaque cas la plus petite somme sensible) soit dépensé de manière, pour chaque bien, qu'il produise la même utilité, ou le même plaisir. Si ce but n'est pas atteint, évidemment l'argent n'est pas dépensé le plus avantageusement possible".

[Copyright Centre Interdisciplinaire Walras-Pareto, Université de Lausanne]